How deep is your code?
Dependency tuples.
Picture your code. Picture all those functions on which there are no source-code dependencies. That might sound odd: if there are no source-code dependencies on a function then what is its purpose? Well, we must distinguish between compile-time dependencies and run-time dependencies. True, all entities at run-time must be called by other run-time entities: it’s turtles all the way down (or at least all the way to freshly powered-up hardware and its firmware-initialized instruction pointer).
In the hyper-modern weirdness of compile-time, however, the source-code dependency is king and two types of function indignantly shun all source-code dependencies. The
first type includes those functions called from outside your source-code. The main() function offers a good example: you write nothing that explicitly calls your main() function, rather the environment smashes into your source-code to find it. The second type includes those functions which implement a signature declared in an interface somewhere else. Clients of such functions seldom if ever call them directly, opting instead to call them via their interface declarations. Yes, the system puts two and two together at run-time to establish what to execute, but at compile-time your system’s flexibility depends on these functions’ being called only via associated interfaces. The source-code dependencies fall on the interface signature, the implementing functions escaping the downpour. (This second type also includes functions inherited from a superclass and called via that superclass but we shall mainly concern ourselves with interfaces here.)
So, back to our visualization. Consider a toy system composed of a single class, Wonder. This class has three functions: Java’s static main() function which instantiates the Wonder object by calling the constructor; the constructor itself, Wonder(); and function a() which is called by the constructor, see figure 1.
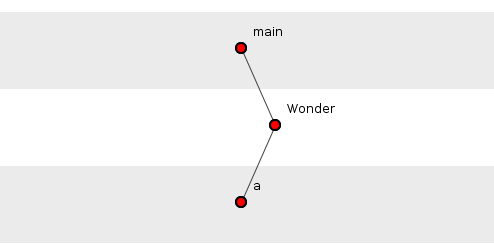
How many source-code dependency tuples are there in figure 1? There is one: {main(), Wonder(), a()}. A tuple is an just ordered set of elements. A source-code dependency tuple, on function-level, is just an ordered set of source-code function dependencies. If these look like plain-old call-paths that is because the two concepts share DNA. Call paths, however, burst to life only at run-time, magical manifestations of conditional execution sequences that leap from implementation to implementation, oblivious to interface. Source-code tuples hibernate in the file-system permafrost, frozen – sometimes for years – between updates. They terminate syntactically on any function that in turn has no source-code dependencies, be it implementation or interface declaration.
Given that the structure of a program on function-level is simply the enumeration of its functions and their inter-relationships, we can say that the function-level structure of a program is in some sense the union of all its function-level dependency tuples. Some further examples may be helpful.
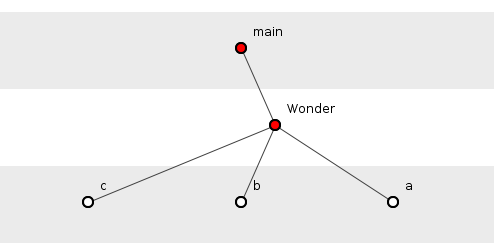
Figure 2 shows a slightly expanded Wonder class, now with the constructor calling three other functions. There are now three dependency tuples: {main(), Wonder(), a()}, {main(), Wonder(), b()} and {main(), Wonder(), c()}.
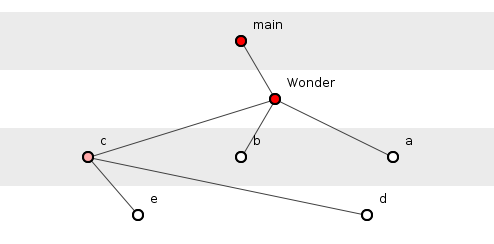
Figure 3 has four dependency tuples. All cosmically interesting, of course, but what has this to do with how, “Deep,” code is?
Code depth.
The depth of a dependency tuple is simply its cardinality, that is, the number of elements it contains. So in figure 3, the tuple {main(), Wonder(), c(), d()} has a depth of four. The depth of a program, then, is the average depth of all its dependency tuples. Thus figure 3 shows a system with a depth of 3.5. Given that a change to a function has a greater probability of rippling back to dependent functions than rippling forward to independent ones, depth interests programmers because the deeper a dependency tuple, the more functions are potentially impacted by changes to that tuple. In figure 3, function e() has three transitively-dependent functions: c(), Wonder() and main(), whereas a() in the shorter tuple has just two.
Code depth, of course, hardly claims to be the only or even the most-important driver of a program’s structure, it merely elbows its way into the rabble of competing influences; but programmers should not ignore it. Let us take a glimpse at the best and worst configurations of our Wonder system, from depth’s perspective.
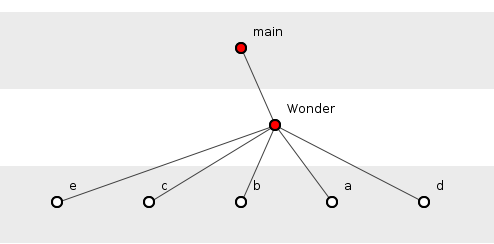
Figure 4 shows the depth-wise ideal configuration of our Wonder functions, that is, the shallowest-possible configuration: the sunburst. (It would be shallower still if we were prepared to tolerate main() function’s calling all others statically.) No function here has more than two functions transitively-dependent on it.
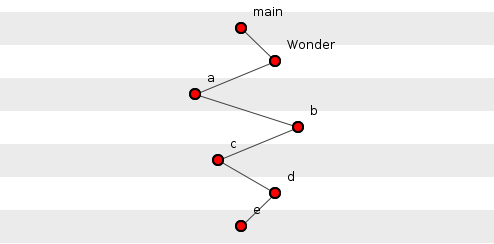
Figure 5, on the other hand, shows the worst configuration for our Wonder system: a single tuple, maximally deep. Five functions here have more than two functions transitively dependent on them. Again, depth remains one of many influencing factors and programmers certainly do not enjoy the freedom to configure their functions any way they wish; at the very least, semantic constraints demand a logical decomposition. So how deep is code? Do programmers keep to the shallows?
Analysis revisited.
Those who have sampled so pitifully small a set as that comprising Junit and Ant should neither draw firm conclusion nor withhold speculation. Figure 6 shows the function-dependency tuple depth of each release of JUnit from version 3.6 to version 4.9.
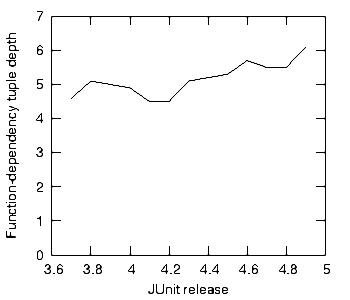
This graphs shows that JUnit maintained an average tuple depth of around 5.5, that is, most functions could expect to reside within a tuple of 5.5 functions (the standard deviation was around three). This hardly seems excessive. Few programmers would find the complexity of such tuples overwhelming. Compare this, however, with Ant’s historical trajectory.
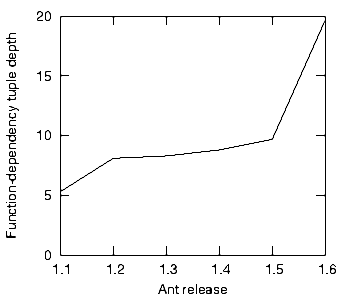
Figure 7 shows Ant’s depth which in version 1.6 has soared to almost twenty (with a standard deviation of around eight). Many programmers might find this suspicious. They might question why most of the functions should find themselves in such long and potentially-ripply tuples. Perhaps more projects should employ depth-guages.
Summary.
Into the pachinko machine of our program we pour the metal balls of our analytical thoughts, watch them bobble and bounce as they fall through webs of intricate dependency tuples and see them collect in the tray with feelings of either satisfaction (“Those functions are structured precisely as they ought to be”) or bewilderment (“That function is connected to what now?”).




